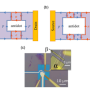
Probing the electrodynamics of graphene using on-chip terahertz spectroscopy. (A) Current carrying modes of a graphene sheet. The zero-momentum mode corresponds to a plasma of counterpropagating electrons and holes and can be relaxed by electron-hole interactions. The finite-momentum mode corresponds to a fluid of co-propagating electrons or holes with nonzero net charge and cannot be relaxed by charge-carrier interactions. The vector J denotes the net current flow. (B) Cartoon of the sample. Photoconductive switches (“emitter” and “detector”) triggered by a pulsed laser emit and detect terahertz pulses within the waveguide. The transmitted pulse is reconstructed by measuring the current collected by the preamplifier (“A”) as a function of delay between laser pulse trains illuminating the emitter and detector. The graphene is optionally excited by a separate pulsed beam (“pump”) to heat the electron system. (C) Photograph of the heterostructure embedded in the waveguide. Few-layer graphene (FLG) electrodes make contact to the monolayer graphene sheet under study and the WS2 gate electrode. Scale bar: 15 micron. Credit: Science, doi:10.1126/science.aat8687
Graphene is expected to behave like a quantum-critical, relativistic plasma known as "Dirac fluid" near charge neutrality in which rapidly collide. In a recent study now published in Science, Patrick Gallagher and co-workers at the departments of physics and materials science in the U.S., Taiwan, China and Japan used on-chip terahertz spectroscopy and measured the frequency-dependent optical conductivity of graphene between 77 K and 300 K electron temperatures for the first time. Additionally, the scientists observed the quantum-critical scattering rate characteristic of the Dirac fluid. At higher doping, Gallagher et al. uncovered two distinct current-carrying modes with zero and nonzero total momenta as a manifestation of .
The work revealed the of the material in which each site is in a quantum superposition of order and disorder (similar to Schrödinger's hypothetical cat in a quantum superposition of 'dead' and 'alive') and the unusual dynamic excitation in graphene near charge neutrality. �鶹��Ժicists consider quantum relativistic effects in the experimental systems influencing condensed matter by the non-relativistic Schrödinger's equation. As a result, previous studies have reported on experimental condensed matter systems such as graphene (a single atomic layer of carbon) in which electron transport was governed by .
defines electron interactions of a typical metal as an ideal gas of non-interacting . In monolayer graphene, this description does not apply due to its structure of linearly dispersing bands and minimally screened Coulomb interactions. Near charge neutrality, graphene is thus expected to host a "Dirac fluid," which is a quantum-critical plasma of electrons and holes that are governed by relativistic hydrodynamics. In lightly doped graphene, a surprising consequence of relativistic hydrodynamics is that current can be carried by two distinct modes; with , also referred to as "energy waves" and "plasmons" in .
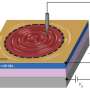
Experimental setup. Left: Large-area photograph of the waveguide device. Right: Cross-sectional view of the heterostructure beneath the waveguide electrodes. Credit: Science, doi: 10.1126/science.aat8687
As doping increased, the weight of the zero-momentum mode was expected to decrease, while that of the finite-momentum mode increased to cross over smoothly from Dirac fluid to Fermi liquid behavior. Previous experiments on clean, monolayer graphene have demonstrated , with examples including studies on low-frequency transport phenomena consistent with hydrodynamic descriptions. Additional experiments indicated - as a signature of the Dirac fluid and as direct evidence of collective motion in a quantum electronic fluid, and the . Even though electron-hole collisions have shown to limit conductivity in charge-neutral bilayer graphene, the direct observation of quantum-critical conductivity of the Dirac fluid has remained elusive.
Experimentally, is an ideal probe across a broad frequency range to observe quantum-critical conductivity, but to lower-quality large-area films, within which . In the present work, therefore, Gallagher et al. leveraged the subwavelength confinement of a to measure the terahertz optical conductivity of graphene, at ten-micron scale thickness within hexagonal boron nitride (HBN). They used the experimental setup to measure the material's conductivity at electron temperatures (Te) ranging between 77 and 300 K to confirm the quantum-critical scattering rate near charge neutrality. The scientists also demonstrated the co-existence of zero- and finite-momentum modes at non-zero doping.
Frequency-dependent optical conductivity of graphene in the Fermi liquid regime. (A) Real and (B) imaginary parts of extracted optical conductivity for several Fermi energies between 46 and 119 meV (electron doping) at 77 K. Solid curves are Drude fits using only the scattering rate τ–1 as a free fitting parameter for each curve. Inset in (A) shows an example of the time-domain current data used to extract conductivity in the frequency domain; the purple trace shows the transmitted waveform at 119 meV, and the black trace shows the transmitted waveform at charge neutrality, which is used as a reference. Inset in (B) shows the extracted τ–1 at lattice temperatures 77 K and 300 K. Credit: Science, doi: 10.1126/science.aat8687
In the experimental setup, Gallagher et al. used photoconductive switches made of semiconducting materials with approximately one picosecond (ps) carrier lifetime to accomplish emission and detection of terahertz pulses. The emitter switch contacting the lower waveguide trace was biased with a dc voltage. When triggered by a laser pulse, the biased emitter became highly conductive for 1 ps. The process injected a current pulse into the coplanar waveguide to interact with graphene prior to reaching a detector switch spanning both traces. In practice, the scientists obtained lower noise by controlling the length of the optical path and detecting the current, to measure the time-domain profile of the transmitted voltage pulse (dV/dt).
After optimizing experimental conditions, the scientists first investigated the optical conductivity of the Fermi liquid at 77 K (T0). The transmitted waveforms contained sharp, sub-picosecond features that evolved with gate voltage to result in maximum transmission at charge neutrality. To extract the optical conductivity from the time-domain data and justify the finite-element simulations, the scientists modeled the device as an infinite, lossless transmission line. Gallagher et al. then probed transport at charge neutrality by observing the change in terahertz transmission (∆V) by optically heating the electron system from T0 = 77 K to varying electron temperatures (Te). To vary temperature in the experimental setup, they adjusted the delay between the optical pump and terahertz probe pulse.
Quantum-critical scattering rate of the Dirac fluid. (A) Real and (B) imaginary parts of the change in optical conductivity at charge neutrality upon optically heating the electron system to a temperature Te above the equilibrium temperature T0 = 77 K. Each curve corresponds to a different delay between the optical pump pulse (fluence 21 nJ cm–2) and terahertz probe pulse. Solid curves are fits to a difference between Drude functions at Te and T0, using Te and the scattering rate τ–1(Te) as free fit parameters for each pair of curves of the complex conductivity. (C) Blue markers indicate the scattering rates and electron temperatures extracted from the fits shown in (A) and (B); error bars indicate standard error in the fits. The experimental scattering rate follows τ–1 = τee–1 + τd –1 (dashed curve), where τee–1 = 0.20kBTe/ħ (green line) is the scattering rate due to charge-carrier interactions, and τd –1 ∝ nimpTe –1 (dotted curve) is the scattering rate due to unscreened, singly charged impurities with density nimp = 2.1 × 109 cm–2. (D) Real and imaginary parts (open and filled circles, respectively) of σ at different Te (i.e., different optical pump delay), replotted as a function of ħω/kBTe. The data for Te = 100 K (21.3 ps delay) do not collapse and are omitted. Credit: Science, doi: 10.1126/science.aat8687
In all measurements, the scientists heavily doped the graphene beneath the waveguide traces to minimize its impedance. The extracted scattering rates at 77 K were below 0.5 and 1 THz, indicating infrequent scattering by disorder and phonons, consistent with of similar doping; thus confirming the anticipated Fermi liquid behavior of graphene. The scientists probed the transport at charge neutrality by observing the change in terahertz transmission. For this, they optically heated the system and calculated the corresponding change in conductivity and the current carried in charge-neutral graphene under experimental conditions. The observed linear evolution in the experiments was a key signature of charge-carrier interactions in the quantum-critical Dirac fluid.
Coexistence of zero- and finite-momentum modes at low doping. (A) Calculated Drude weights DZ and DF of the zero- and finite-momentum modes (27) in lightly electron-doped (εF = 33 meV) and undoped graphene. (B) Real and (C) imaginary parts of the measured change in optical conductivity when charge neutral graphene in equilibrium (T0 = 77 K) is simultaneously heated to an electron temperature Te (optical pump delay 3 ps, fluence 21 nJ cm–2) and doped to εF = 33 meV. (D) Real and (E) imaginary parts of the measured change in optical conductivity when charge neutral graphene at an electron temperature Te (optical pump delay 4 ps, fluence 20 nJ cm–2) is doped to various εF. Data at each doping are well fit by a single Drude function (solid curves) describing the conductivity of the finite-momentum mode with free fit parameters Te = 267 ± 3 K and τd –1(εF) ~ 1 THz. Inset in (D) shows the scattering rate for the finite momentum mode τd –1 versus Te extracted from fits at varying Te. Colors indicate εF as in (D), (E). Credit: Science, doi: 10.1126/science.aat8687
In this way, Gallagher et al. elegantly demonstrated the quantitative agreement between the experimental results and relativistic hydrodynamic theory of the Dirac fluid graphene. The scientists implied that graphene should host relativistic phenomena that are not observed in typical electron systems (to which relativistic hydrodynamics do not apply). For instance, in conventional metals, electronic sound waves either morph into plasmons or are destroyed by momentum relaxation. However, the new results indicate that such waves can exist in charge-neutral graphene as a result of low disorder and zero-coupling to . The experimental work by Gallagher et al. thus provided access to the subtle and rich physics of relativistic hydrodynamics of graphene in a bench top experiment. Further experiments can investigate the of graphene at in the future.
Written for you by our author —this article is the result of careful human work. We rely on readers like you to keep independent science journalism alive. If this reporting matters to you, please consider a (especially monthly). You'll get an ad-free account as a thank-you.
More information: Patrick Gallagher et al. Quantum-critical conductivity of the Dirac fluid in graphene, Science (2019).
K. S. Novoselov et al. Two-dimensional gas of massless Dirac fermions in graphene, Nature (2005).
© 2019 Science X Network