麻豆淫院

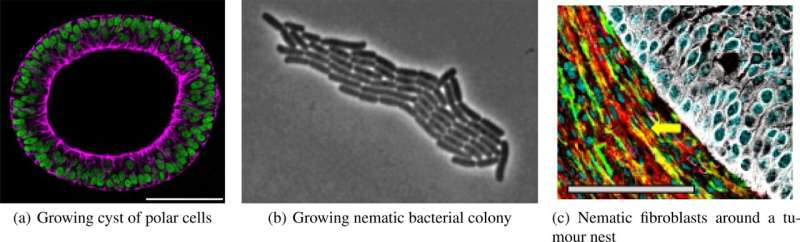
A key feature of biological tissues is their inhomogeneity and their ability to grow via cell reproduction. To study this behavior, it is important to describe it using equations, which account for factors including growth rates, chemical signaling, and tissue structure.

Researchers from Paris aim to develop consistent continuous descriptions of these deeply complex systems: accurately predicting properties such as cell reproduction rates, disorder, and how their growth varies in different space directions, depending on their interactions.

Through their new analysis in The European 麻豆淫院ical Journal Plus, Joseph Ackermann and Martine Ben Amar at Sorbonne University Paris, show that tissue development can be reliably captured within "Onsager's variational principle," a mathematical framework used widely in thermodynamics.

Their approach could lead to a deeper understanding of tissue properties across a wide array of scenarios, from essential processes such as embryo development, to harmful ones such as tumor growth.

In thermodynamics, Onsager's variational principle describes how systems tend towards a state of minimum dissipation as they are continually altered by their own transformations and their environment. Mathematically, the principle expresses these systems as groups of interconnected equations, each describing the rates of change of certain quantities describing them.

Starting from Onsager's variational principle, new "momentum" and growth equations are derived, which could better describe the flow of mass and the proliferation, as well as the orientations of cells in biological tissues. Their equations considered the growth and death rates of cells, as well as the chemical reactions driving their activity. This approach could also illustrate the genesis of patterns in growing organs.

Altogether, the duo's work definitively shows how Onsager's variational principle can be a valuable tool for exploring different theoretical scenarios in growing tissues, and how their growth depends on interactions between different cellular-scale properties.