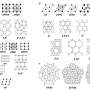
Mathematicians introduce crossing matrices to decode doubly periodic weaves

Doubly periodic weaves—entangled structures with repeating patterns in two independent directions—pose a mathematical challenge. Originally conceived to model real-world structures, such as woven textiles and molecular weaving of polymers, mathematicians have generalized the theory to include weaves with any number of distinct directions, extending beyond practical weaving to a broader topological framework.
However, one major obstacle has been the lack of suitable invariants to classify periodic weaves consistently. Traditional knot invariants struggle to capture the complexity of repeating patterns, particularly in distinguishing different weaves or defining minimal units for analysis.
In in the Journal of Knot Theory and Its Ramifications, Sonia Mahmoudi and co-workers from AIMR introduced crossing matrices and adapted the concept of crossing numbers to periodic structures. These tools offered a framework for the topological classification of doubly periodic untwisted weaves, bridging gaps in prior approaches by including both biaxial and triaxial weaves.
"The use of crossing matrices enabled us to encode the arrangement of crossings in periodic weaves systematically and to compute their crossing number within their minimal unit cells," explains Mahmoudi. "This provided a robust combinatorial method for analyzing and classifying these topological structures."
The team demonstrated this by calculating the total crossing number of a weave precisely and by establishing equivalence classes of weaves through cyclic permutations of matrix rows and columns.
These results paved the way for advancements—beyond mathematics—in materials science, such as creating more resilient fabrics or designing nanostructures with tailored properties.
Future research aims to extend these methods to more complex periodic entanglements, opening exciting new possibilities in both theoretical and applied sciences, including technical fabrics, molecular weavings, and metamaterials.
Provided by Tohoku University