Â鶹ÒùÔº

Statistical mechanics is one of the pillars of modern physics. Ludwig Boltzmann (1844–1906) and Josiah Willard Gibbs (1839–1903) were its primary formulators. They both worked to establish a bridge between macroscopic physics, which is described by thermodynamics, and microscopic physics, which is based on the behavior of atoms and molecules.

The Austrian physicist Boltzmann explained the second law of thermodynamics in statistical terms. He defined the entropy of a system based on the number of possible microstates it could assume.

Unlike Boltzmann, who focused more on the physics of gases and the distribution of particles in equilibrium, the American Gibbs developed a general mathematical formalism that could be extended to more complex systems. Together, their contributions formed the basis of a physics capable of modeling a wide variety of phenomena.

However, Boltzmann-Gibbs statistical mechanics has limitations. For example, its predictions can fail when a system is in certain regimes, such as phase transitions or critical phenomena. For instance, statistical mechanics predicts the divergence of certain thermodynamic quantities at critical points, which is not observed experimentally. This has led to the development of the so-called "non-extensive statistical mechanics," a generalization of Boltzmann-Gibbs-von Neumann-Shannon statistical mechanics proposed by the Greek-Brazilian physicist Constantino Tsallis.

A new study led by Mariano de Souza at São Paulo State University (UNESP), in collaboration with Constantino Tsallis at the Brazilian Center for Â鶹ÒùÔºics Research (CBPF), has focused on the problem of divergence at critical points. The results are in the journal Â鶹ÒùÔºical Review B.

"Entropy quantifies the number of possible microstates of a system. In the context of Boltzmann-Gibbs statistical mechanics, this entropy is extensive, i.e., it grows proportionally to the size of the system. However, at critical points and phase transitions, this extensiveness can be violated due to the emergence of long-range correlations between particles," says Souza. "This means that the traditional approach predicts the divergence of quantities such as isothermal magnetic susceptibility and the coefficient of thermal expansion, something that does not match experimental reality.

"A widely used tool for studying these phenomena is the Grüneisen parameter (Γ), which relates thermal expansion to the specific heat of the material. According to Boltzmann-Gibbs statistical mechanics, this parameter should also diverge at critical points. However, in practice, it isn't possible to measure infinite values for physical quantities, indicating that the theory needs to be regularized."

In 1988, based on the concept of multifractals, Tsallis proposed a generalization of the Boltzmann-Gibbs-von Neumann-Shannon entropy, known as non-additive entropy S_q. This formulation introduces an entropic index (q), which makes it possible to adjust how probabilities are accounted for when calculating entropy.

Under normal circumstances, the Boltzmann-Gibbs theory remains valid. However, in systems exhibiting critical phenomena, a specific value of q can restore the extensiveness of the entropy and eliminate the divergences predicted by the traditional theory.

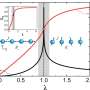
"Inspired by this approach, we reformulated the Grüneisen parameter in S _q terms. To do this, we used the quantum version of the Grüneisen parameter, Γ^0K, to study one of the simplest models with a quantum critical point: the one-dimensional Ising model under the action of a transverse magnetic field, as shown in Figure 1.

"The results showed that the limit of Γ ^0K is infinite for q > q_special, zero for q < q_special, and finite and non-zero only for q = q_special, where q _special is the value of the index q that recovers the extensiveness of the entropy.

"In other words, while conventional theory predicted divergence at critical points, the new approach based on non-additive entropy regularizes these divergences and provides finite values consistent with experimental observations," says Souza.

The results of the study offer new insights into critical phenomena in complex systems. The regularization of the theory can be applied to a variety of systems, from magnetic materials to condensed matter systems and quantum fluid dynamics.

"We believe that this approach can provide valuable insights into critical phenomena in different contexts," comments Souza.

In addition to Souza and Tsallis, the study featured the participation of master's student Samuel Martignago Soares and postdoctoral student Lucas Squillante, both from Souza's team, as well as postdoctoral student Henrique Santos Lima from the CBPF.