Â鶹ÒùÔº

There has long been a mystery when calculating how an incoming light wave scatters off an object and becomes a modified, outgoing light wave. In particular, the time delay of the transition from one to the other comes out to be a complex number, a regular real number but with a nonzero imaginary part.

The imaginary part of the is a regular real number times the square root of -1, designated by "i." Â鶹ÒùÔºicists have found that the first part, the regular real number (usually a mathematical function of energy, or frequency), is predicted well, but they have been so puzzled by the imaginary part, and a bit embarrassed, that they deemed it "unphysical" and ignored it.

But now a pair of physicists from the University of Maryland in the U.S. have shown that the complex part does indeed have a meaning, related to the frequency shift of the transition from incoming to outgoing wave. Their work has been in Â鶹ÒùÔºical Review Letters.

The mathematical function that describes the linear transition from one wave function to the other is called the scattering matrix or S-matrix. The scattering matrix, a square array with as many rows and columns as the number of channels of the incoming wave, in principle contains all there is to know, scattering-wise, about the system doing the scattering, which may be glass such as a frosted window or lens, water, a fiber optic cable, atomic nuclei, atoms, molecules and many-body quantum systems.

Inside the system, the light wave's velocity typically changes; such a system is called a "dispersive medium." In particular, the scattering matrix for a dispersive medium can provide the time delay of the wave's transition from incoming to outgoing—how long the wave stays in the system.

The time delay, in turn, provides scientists, engineers and technicians with parameters such as the phase evolution of quantum waves, the delay of a wave group in a fiber optic cable and the group delay in waveguides, among other quantities.

But what to make of the imaginary parts of the scattering matrix? In a in Nature Communications by lead author M. Asano of Japan, a group of scientists from several countries around the world recognized that for light pulses that meet certain requirements, the imaginary part of the scattering matrix—more precisely, the real number before "i," the square root of -1—represented the "frequency shift" of the transitioning wave due to its passage through the scattering system. In particular, it represents the shift of the frequency in the center of the pulse (shaped as a Bell curve, a Gaussian distribution) of the incoming light pulse.

The requirements are straightforward and not uncommon. The frequency bandwidth, or range of frequencies in the pulse, must be small and the scattering system must be linear and dispersive—that is, the outgoing wave channels are a linear sum of the incoming wave channels, proportional to each—and the properties of the scattering system depend on the incoming wave's frequency components. (It is equivalent when discussing the scattering system's effects in terms of wavelengths or energies.)

The co-authors of the current paper in Â鶹ÒùÔºical Review Letters, Isabella L. Giovannelli and Steven M. Anlage of the Maryland Quantum Materials Center at the University of Maryland decided to check this theoretical prediction.

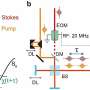
For their experiments they used a two-port microwave ring graph as the scattering system. This device is a resonator, a closed loop waveguide in which electromagnetic waves circulate (the microwaves) and form patterns where the circumference of the ring is an integer number of wavelengths.

Ring graphs are often used as filters or switches. The actual ring consisted of two coaxial cables of different lengths, 28 cm and 31 cm long, and two T-junctions.

The microwave pulses sent through the ring graph had a center frequency of 5 gigahertz (a standard microwave oven uses microwaves of 2.45 GHz), with a narrow bandwidth of only 5 megahertz (0.005 GHz).

The experimentalists chose a frequency domain setup for their measurements, meaning the light pulses were analyzed as functions of frequency—how much of each frequency is present. The alternative is a time domain setup, where the signals are analyzed as functions of time— how the signal's amplitude changes over time. The frequency domain setup uses electronics which apply mathematical transforms to show amplitude and phase as functions of frequency.

In this way, the pair sent the 5 GHz microwaves through the resonator and measured the time delay of the wave pulse to be -7.95 nanoseconds (ns), and a shift in frequency of the center of the pulse's Bell curve of 0.48 megahertz.

The prediction for the imaginary time delay, or frequency shift, is 3.03 radians per microsecond, which is 0.482 million cycles per second or 0.482 MHz. The measured frequency shift is, they write, "in excellent agreement with the predictions of Asano et al."

With the confirmed theory, "we can now make predictions for reflection time delays, along with reflection time-delay difference," they conclude, among other time delay differences in more complicated systems.

© 2025 Science X Network