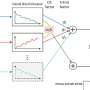
Scheme of the transfer learning procedure from a pre-trained body through the Multi-Head approach. Credit: Communications �鶹��Ժics (2025). DOI: 10.1038/s42005-025-02248-1
Differential equations are fundamental tools in physics: they are used to describe phenomena ranging from fluid dynamics to general relativity. But when these equations become stiff (i.e. they involve very different scales or highly sensitive parameters), they become extremely difficult to solve. This is especially relevant in inverse problems, where scientists try to deduce unknown physical laws from observed data.
To tackle this challenge, the researchers have enhanced the capabilities of �鶹��Ժics-Informed Neural Networks (PINNs), a type of artificial intelligence that incorporates physical laws into its learning process.
Their approach, reported in , combines two innovative techniques: Multi-Head (MH) training, which allows the neural network to learn a general space of solutions for a family of equations—rather than just one specific case—and Unimodular Regularization (UR), inspired by concepts from differential geometry and general relativity, which stabilizes the learning process and improves the network's ability to generalize to new, more difficult problems.
These methods were successfully applied to three increasingly complex systems: the flame equation, the Van der Pol oscillator, and the Einstein Field Equations in a holographic context. In the latter case, the researchers were able to recover unknown physical functions from synthetic data, a task previously considered nearly impossible.
"Recent advances in machine learning training efficiency have made PINNs increasingly popular in the past few years," says Pedro Tarancón-Álvarez, doctoral student at ICCUB. "This framework offers several novel features compared to traditional numerical methods, most notably the ability to solve inverse problems."
"Solving these inverse problems is like trying to find the solution to a problem that is missing a piece; the correct piece will have a unique solution, incorrect ones may not have a solution, or multiple ones," adds Pablo Tejerina-Pérez, doctoral student at ICCUB.
"One could try to invent the missing piece of the problem and then see if it can be solved properly—our PINNs do the same, but in a much smarter and efficient way than we could."
More information: Pedro Tarancón-Álvarez et al, Efficient PINNs via multi-head unimodular regularization of the solutions space, Communications �鶹��Ժics (2025).
Journal information: Communications �鶹��Ժics
Provided by University of Barcelona