Â鶹ÒùÔº

Â鶹ÒùÔºicists can explore tailored physical systems to rapidly solve challenging computational tasks by developing , combinatorial optimization and focusing light through scattering media. In a new report on Science Advances, C. Tradonsky and a group of researchers in the Departments of Â鶹ÒùÔºics in Israel and India addressed the phase retrieval problem by reconstructing an object from its scattered intensity distribution. The experimental process addressed an existing problem in disciplines ranging from X-ray imaging to astrophysics that lack techniques to reconstruct an object of interest, where scientists typically use indirect iterative algorithms that are inherently slow.

In the new optical approach, Tradonsky et al conversely used a digital degenerate cavity laser (DDCL) mode to rapidly and efficiently reconstruct the object of interest. The experimental results suggested that the gain competition between the many lasing modes acted as a highly parallel computer to rapidly dissolve the phase retrieval problem. The approach applies to two-dimensional (2-D) objects with known and complex-valued objects, to generalize imaging through scattering media, while accomplishing other challenging computational tasks.

To calculate the intensity distribution of light scattered far from an unknown object relatively easily, researchers can compute the source of the absolute value of an object's . The reconstruction of an object from its scattered intensity distribution is, however, ill-posed, since phase information can be lost and diverse phase distributions in the work can result in different reconstructions. Scientists must therefore obtain prior information about an object's shape, positivity, spatial symmetry or sparsity for more precise object reconstructions. Such examples are found in , studies, , , and when . During the reconstruction of objects with a finite extent (compact support), researchers offer a unique solution to the phase retrieval problem, as long as they model the same scattered intensity at a .

Â鶹ÒùÔºicists had developed several algorithms to solve the phase retrieval problem in the last decade, including the algorithm, and (RAAR). However, they are based on iterative projections that are relatively slow even . As an alternative, research teams can address computational challenges using specifically tailored physical systems. While such systems are not universal Turing machines (i.e., they cannot perform arbitrary calculations), they can potentially solve a efficiently. Solving difficult problems with such systems compared to the use of conventional computers.

Tradonsky et al experimentally demonstrated a new optical system to rapidly solve phase retrieval problems based on a (DDCL). The device incorporated two constraints, including the Fourier magnitudes of scattered light from an object and the compact support. The nonlinear lasing process within the cavity resulted in a self-consistent solution that satisfied both constraints. The underlying physical mechanism in the DDCL was similar to that observed with (OPO) spin stimulators.

Both OPO simulators and DDCLs have performed optimizations via with ability to and possessed a . The scientists facilitated the compact support aperture within the cavity to ensure different configurations of laser phases to result in different losses, to allow the configuration with minimal losses to win the mode competition and solve the phase problem. The DDCL system contained many attractive and important features including high parallelism to provide millions of parallel experimental realizations, short round trip times approximating 20 nanoseconds, fast convergence times and an inherent selection mode that accounted minimal loss owing to mode competition. In theory, of all the time-evolving phase configurations, the one with the highest energy won the mode competition relative to the limited gain. As a result, larger the number of initial independent configurations in practice, higher the probability of the system to find a correct solution with a stable configuration and no losses.

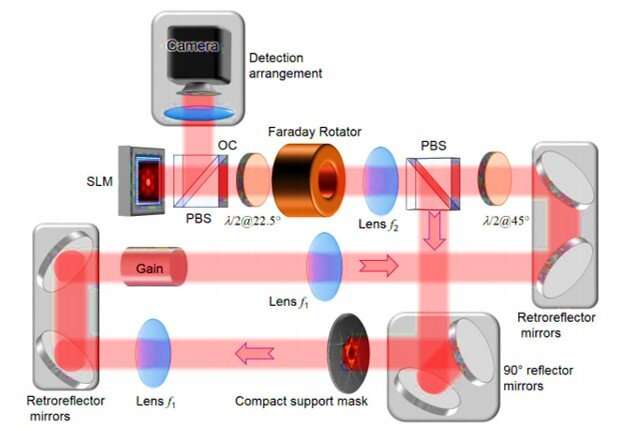
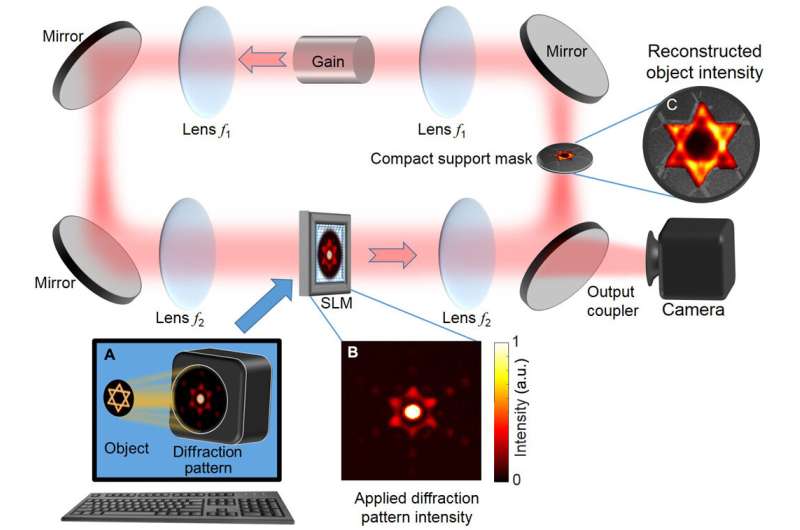
In the experimental setup, Tradonsky et al included a ring degenerate cavity laser with an inherent gain medium, two 4f telescopes and an amplitude spatial light modulator (SLM). The system also included an intracavity aperture, 3-D reflectivity mirrors and an output coupler. The team used the left 4f telescopes to image the center of the gain medium onto the SLM and , independently. They combined the intracavity aperture with the SLM to control and form the output . When the scientists placed an intracavity aperture (compact support mask) at the Fourier plane between the two lenses, each phase distribution demonstrated a different level of loss. Consequently, the phase distribution with minimal loss was the most probable lasing mode in the study. The team considered two figures of merit to quantify the quality of the system including solution fidelity and computation time. The research team obtained representative results for objects with very good agreement between intensity distributions of the original (actual object) and reconstructed forms.

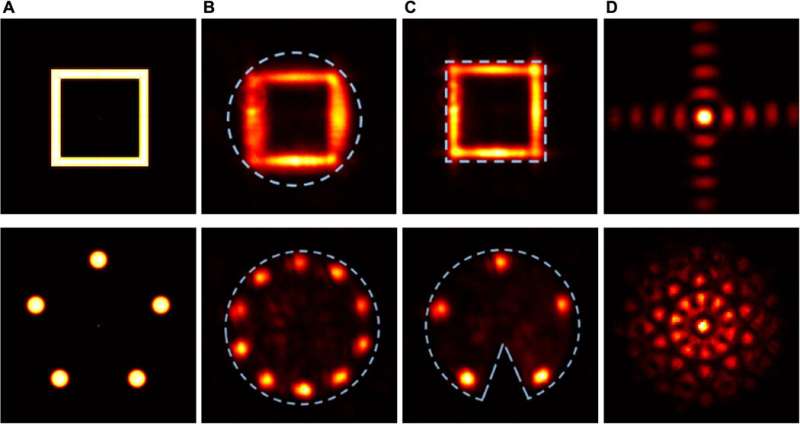
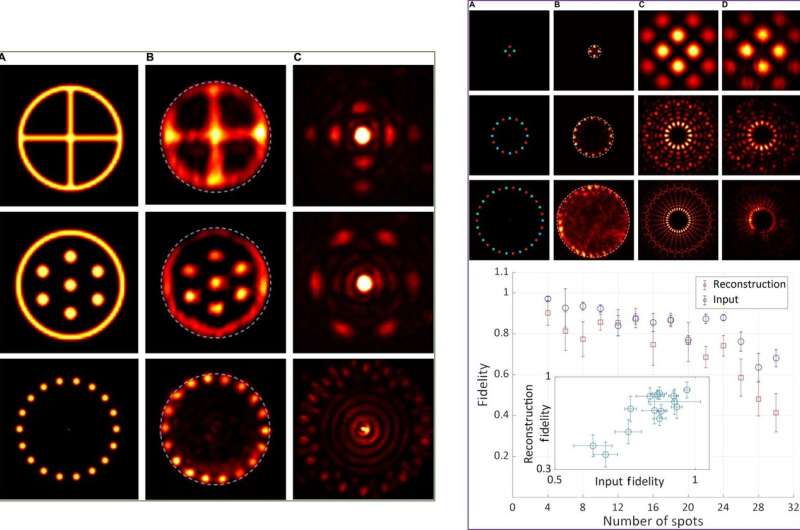
Tradonsky et al measured the effect of object complexity on reconstruction fidelity and formed representative intensity distributions for objects with four, 16, and 30 spots. The results showed that higher complexity objects (those with more spots) showed higher-complexity Fourier intensity distribution, with intricate detail that could not be resolved using the present system. They also noted the input and reconstruction fidelities to decrease with increasing object complexity, which they credited to the fluctuating technical noise of the laser pump. They conducted qualitative experiments to assess the effect of tightness and symmetry during object reconstruction. The results showed that a tight compact support significantly improved the quality of the reconstructed object.

The team then investigated the quantitative effects of the radius of the compact support aperture on the quality and fidelity of reconstruction. For bigger objects the representative intensity underwent rapid decay during reconstruction fidelity since the laser was unable to support the object shape. With objects smaller than the compact support aperture, Tradonsky et al observed slower decay in fidelity. In total, they observed reduced reconstruction fidelity when the camera averaged across multiple realizations of an object within the system.

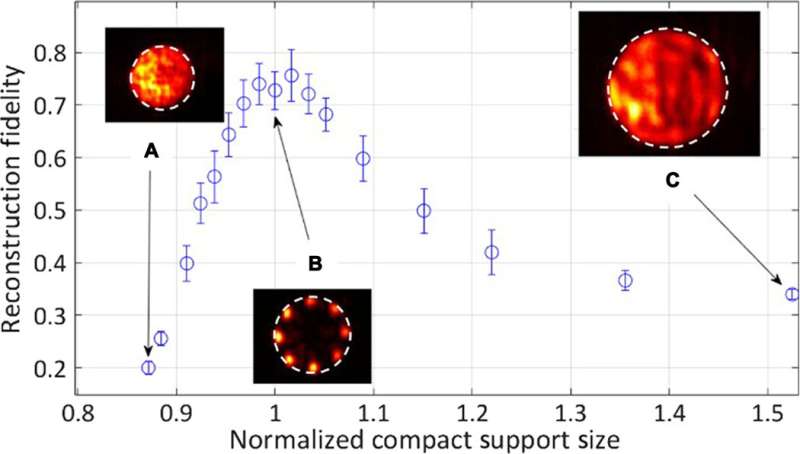
Generally, the resolution of the reconstructed objects was relatively low due to phase aberrations in the laser cavity. The team proposed to optimize the system and reduce aberrations for improved resolution. The scientists also analyzed the time taken to offer a reconstruction solution using the system and found the durations dictated by the SLM (spatial light modulator) and the camera readout to approximate 20 ms. The actual computation time of lasing only lasted less than 100 nanoseconds. When Tradonsky et al optimized the experimental setup using a Q-switched linear degenerate cavity laser arrangement with pockel cells, they reduced the total computation time of the system to approximately 100 nanoseconds. Comparatively, the reconstruction time with the RAAR algorithm lasted one second.

In this way. C. Tradonsky and colleagues presented an optical system for rapid phase retrieval using a new DDCL (digital degenerate cavity laser). The computation time amounted to 100 nanoseconds; orders of magnitudes faster than conventional, algorithm based computational systems. Based on the results, several modifications to the DDCL system can potentially improve its performance, including increased length of the laser cavity to increase the number of independent parallel investigations. The research team will further explore the system to solve a variety of problems and resolve imaging quality after .

© 2019 Science X Network